728x90
최적화는 여러 공학 분야에서, 일상에서도 많이 쓰이지만 명확하게 의미를 파악하는 것이 어려웠습니다. 지금까지 공부를 하며 제가 이해한 최적화라는 개념의 의미와 기계학습 분야에서 최적화의 의미를 설명하는 포스팅을 남깁니다.
- Optimization수치해석 교과서1에서 optimization은 특성을 나타내는 함수의 최대값이나 최소값을 만드는 입력을 찾는 것이라고 설명하고 이 값을 optimal value라고 설명합니다.

- optimal value라고 하면 가능한 조건(domain)에서 가장 좋은 최적의 값이라고 생각할 수 있다.
- 최적화를 활용해 설계를 하고자 하면 최적 설계, 제어를 하고자한다면 최적 제어가 된다. 이렇게 공학적인 내용 뿐만아니라 물자 조달과 같은 실생활에 밀접한 문제도 최적화를 통해 해결을 한다.
- 최적화를 하기 위해서는 위와 같이 조건에 따라 상황이 얼마나 좋은지 비교할 수 있는 함수가 필요하다. 이를 목적 함수라고한다.
- 최소화 하는 최적화 문제에서는 loss 혹은 cost function이라고, 최대화 하는 최적화 문제에서는 그냥 objective function이라고 부르는 것 같다.
예를 들면
- 두 사람 A와 B가 좋은 자동차 여행지를 선택하는 문제를 생각해보자. 행복(happiness)을 최대화 하는 여행지를 선택해보자. 우선 여행지 최적화의 목적 함수인 행복을 정의해야한다.
- 먼저 A는 운전 거리가 멀어지면 피곤함(fatigue)으로인해 행복은 떨어진다. 이를 1km당 0.01의 행복이 떨어지는 것으로 모델링하면 $fatigue = 0.01\times x$이다. 피로도는 행복에 부정적인 영향을 주기 때문에 $happiness = -fatigue$로 피로도를 고려한 행복을 정의했다.그런데 이렇게 행복을 정의하면 여행을 안가는게 최고의 여행이라는 결과가 나오게 된다.

- B는 여행을 떠날 때 처음에는 신나지만 운전을 오래 하다보면 지나치는 풍경도 익숙해지고 점차 심심해진다. 이런 비선형적인 행복을 모델링하기 위해 재미(fun)를 모델링하면 $fun = log(x+1)$로 모델링 할 수 있다. 재미는 행복에 긍정적인 영향을 주기 때문에 $happiness = fun$으로 재미를 고려한 행복을 정의한다면 멀리 갈수록 좋은 여행지라는 결론을 얻게된다.

- A와 B가 함께 가는 여행에서 최적의 여행지를 선택하려면 피로와 재미를 같이 고려한 만족감을 정의하고 최적값을 찾아야한다. 둘을 함께 고려하고자 하면 $happiness = fun -fatigue$로 목적함수를 정한다면 다음과 같은 형태를 얻는다.

- 만약 A와 B가 서로 얼마나 배려를 해주는지에 따라서 재미를 더 추구하거나 피로를 더 고려할 수 있다. 배려의 정도는 각각의 요소에 weight를 부여하는 것으로 이해할 수 있다. $(happiness = w_1\times fun -w_2 \times fatigue)$로 목적함수를 결정해 여행지 최적화를 할 수 있다. A가 조금 양보해 재미를 조금 더 추구하고자 $w_1 = 1.1$, $w_2 = 0.9$로 부여하면 조금 더 멀리 여행을 갈 수 있다.

Machine learning 개념3
- 모델을 학습한다는 것은 데이터를 활용해 좋은 모델의 파라미터를 찾는 것을 의미한다. 지도학습의 경우에는 데이터의 input과 output 간의 관계를 가장 잘 나타내주는 모델의 파라미터를 찾아가는 것이다.
- 우선 다음과 같이 ((x,y))로 이루어진 데이터가 주어져 있다고 하자.

- 지도학습 중 간단한 선형회귀에 예를 들어보면 선형 모델은 $\hat{y}=w_1 x+ w_2$로 표현된다. 선형 모델은 weight($w_1$)와 ($w_2$)에 의해서 결정이 되고, 이를
모델 파라미터라고 한다. 파라미터가 존재할 수 있는 공간을 parameter space라고 하는데, 여기에서는 ($w_1$)과 ($w_2$)가 만드는 2차원 공간이 된다. weight에 의해 다음과 같이 많은 선형 모델들이 결정된다.
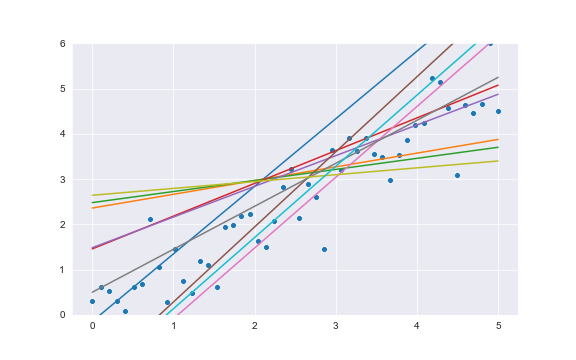
- 선형 모델을 학습한다는 것은 이 무한한 공간에서 주어진 데이터를 가장 잘 설명하는 최적의
모델 파라미터를 찾는 과정을 학습이라고 한다. 이 과정에서 최적화가 필요하다. 회귀 모델에서 데이터를 잘 설명한다는 것은 x가 주어졌을 때 y값을 잘 예측하는 것이다. - $error(w_1,w_2) = \sum{(\hat{y}(x_i ;w_1,w_2) - y_i)^2}$로 오차를 정의하면 학습은 오차를 모델을 만드는 파라미터 $w_1, w_2$를 찾는 문제로 정의할 수 있습니다. 데이터는 결정되어 있는 값이기 때문에, error는
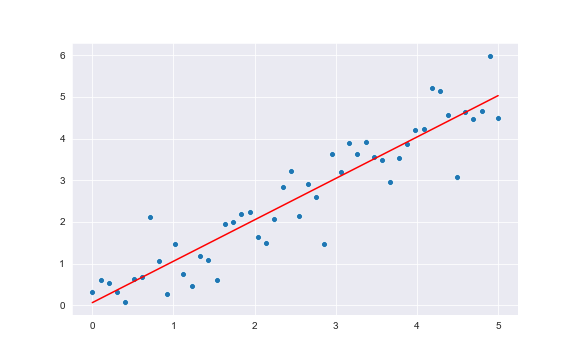
모델 파라미터에 대한 함수입니다. - 이 error를 최소화하는 $w_1$, $w_2$를 찾는 과정이 학습입니다. 일반적으로 이런 error와 같은 함수를 loss function이라고 하고 모델을 학습한다는 것은 loss function을 최적화 하는 과정을 의미합니다.
- 이 과정은 sklearn 라이브러리를 활용하면 다음의 코드로 쉽게 구현할 수 있습니다.
- 앞의 최적의 여행지를 찾는 최적화 문제에서 목적함수에 의도를 반영했던 것 처럼 머신러닝, 딥러닝의 loss function을 조작하는 것은 간단하게는 과적합을 방지하는 regularization부터 GAN, Domain adaptation 등의 방법에까지도 필요합니다.
하이퍼파라미터 최적화4,5
- 모델 학습 과정에서 학습되는 파라미터 외에 사용자가 지정해주는 파라미터를
하이퍼파라미터라고 합니다. 주요한하이퍼파라미터에 따라 모델의 성능의 차이가 발생하기 때문에 적절하게 튜닝을 해주어야 한다.하이퍼파라미터도 여러 값을 바꿔가며 튜닝을 해주어야 한다. 하이퍼파라미터공간을 탐색하는 방법 중 가장 흔하게 사용되는 방법들은 다음과 같다.- Grid search :
하이퍼파라미터공간을 격자 형태로 분할하고 모든 격자점에서 모델의 성능을 비교하는 방법. Grid search는 탐색하고자 하는 공간을 골고루 탐색할 수 있다는 장점이 있지만 모델 성능에 큰 영향을 주지 않는하이퍼파라미터까지 탐색해 비효율을 야기할 수 있다. - Random search :
하이퍼파라미터공간에서 랜덤하게하이퍼파라미터를 샘플링하고 모델의 성능을 비교하는 방법. Random search는 공간 전체를 균일하게 탐색하는 방식 대신 완전히 랜덤하게 탐색하는 방식으로 앞의 grid search의 비효율을 야기하지 않는다. 그렇지만 랜덤하게 탐색하는 방식이기 때문에 효율적인 방법은 아니다. - Bayesian search : bayesian optimization 방법을 활용해 최적화하는 방법. bayesian rule에 기반해 탐색한
하이퍼파라미터의 결과를 반영한 새로운 탐색 공간을 제안하는 방식으로 진행되기 때문에 세가지 방법 중 가장 효율적인 방법이라고 생각한다.
- Grid search :
- 그리드 서치, 랜덤서치는 sklearn에서, bayesian search는 skopt을 사용해 구현할 수 있고, 교차 검증과 최적화를 한번에 수행해주는 method도 구현되어 있어 편리하게 사용할 수 있다.
- 2017년에 Hyperband 방법의 논문이 출판되었는데 이는 아직 공부를 못했지만 keras-tuner에는 구현되어 있어 사용할 수 있다.
마무리
- 학습시 loss function을 조작하는 이유와 효과를 이해할 수 있도록 머신러닝을 공부하며 자주 등장하는
최적화개념을 설명했다.
Reference
[1] Applied Numerical Method with MATLAB for Engineers and Scientists
[2] 수학적 최적화 - wiki
[3] 서울대학교 윤성로 교수님 강의 - youtube
[4] hyperparameter optimization 방법 설명 - Toward datascience
[5] Li, Lisha, et al. "Hyperband: A novel bandit-based approach to hyperparameter optimization." The Journal of Machine Learning Research 18.1 (2017): 6765-6816.
[6] pyforest 라이브러리 설명
'Data science' 카테고리의 다른 글
| 신뢰성 공학 기초 (0) | 2023.10.04 |
|---|---|
| 모델과 지도학습 (0) | 2023.08.30 |
| 인공지능과 수학 (4) | 2023.08.06 |
| Affine 변환 (0) | 2022.07.24 |
| 클래스 불균형 다루기 (0) | 2022.07.20 |