모델이란

모델링은 현실 세계의 시스템, 현상의 간소화된 표현을 생성하는 과정으로 이를 통해 현실 세계를 이해, 분석, 예측 및 최적화를 할 수 있다. 대부분의 모델은 ‘예측’을 목적으로 한다. 여러 변수 간의 관계를 방정식, 알고리즘 등으로 정의해 실제로 만들어 관측하기 전에 자극
Physics-based model
물리 기반 모델은 물리적인 법칙에 의해 만들어진 모델이다. 지금까지 과학 시간에 배웠던 가장 유명한 물리 모델은 힘과 운동의 관계를 기술한

이 모델을 통해 현재 상태가 주어졌을 때 물체의 과거 시점과 미래 시점의 위치, 속도, 가속도를 추정하거나 예측할 수 있다.
Data-driven model
데이터 기반 모델은 관측된 데이터의 분석의 결과로 만들어진 모델을 말한다. 데이터 내의 변수들의 관계를 가장 잘 설명하는 수식이나 규칙을 찾는 방식의 모델링 결과를 데이터 기반 모델이라고 할 수 있다. 16~17세기 케플러 1법칙인 타원 궤도 법칙의 연구 과정을 데이터 기반 모델링으로 볼 수 있다. 케플러는 뉴턴의 운동 법칙이 세상에 나오기 전에 티코 브라헤의 관측 데이터만을 가지고 공전 궤도의 수학적인 모델을 찾아냈다. 그 외에 확률과 통계 시간에 배운 확률 분포부터 머신러닝 알고리즘까지 모두 data-driven model이라고 할 수 있다.
지도 학습이란
지도 학습은 통계적 학습 방법 중 예측과 추론을 목적으로 하는 학습 방식 중 하나로 데이터의 특징인 Feature
지도학습의 가정은 feature와 label은 어떤 관계
분류와 회귀
지도 학습 문제는 label의 데이터 형태에 따라 분류와 회귀로 나눌 수 있다. label이 연속적이고 무한한 값을 가질 수 있는 경우 회귀, 불연속적이고 유한한 값을 가질 수 있는 경우 분류라고 한다. 분류 문제의 label을 각각의 unique한 값은 class라는 이름으로도 불린다. titanic호에 탑승한 승객의 나이, 성별, 좌석의 위치 등으로 생존 여부
머신러닝 알고리즘
지도 학습의 아이디어를 실현 할 수 있는 많은 머신러닝 알고리즘이 존재한다. 각각의 알고리즘은 고유한 방식에 따라 입력 feature
parametric method는 아래 선형 회귀와 같이 parameter가 존재해 parameter값에 따라 모델이 결정되고, non-parametric method는 선형 보간처럼 입력된 데이터에 따라 모델이 결정된다. parametric은 학습 과정에서 데이터에 따라 parameter를 조정해 데이터의 관계를 잘 설명하는 모델을 찾고, non-parametric은 학습 과정에서는 학습 데이터를 모델에 저장한 후 예측 과정에서 추론 알고리즘에 따라 예측을 반환한다.
유명한 parametric method의 지도 학습 모델은 다음과 같다.
- 선형 회귀
- 로지스틱 회귀
- Support Vector Machine
- Decision tree와 random forest
- Neural network model
( )
모델의 학습과 최적화 : 선형 회귀 모델의 예시
parametric model의 학습을 이해하기 위해 랜덤으로 생성한 5개의 데이터에 대해 가장 간단한 예측 모델인 선형 회귀 모델의 학습 과정을 살펴보자.
선형 회귀 모델
선형 회귀 모델은 feature들에 대한 가중 합
여기에서 x들과 y는 데이터, w는 weight로 모델 파라미터이다. 식에서 알 수 있듯 x 데이터를 입력받아 가중치에 따라 조정된 값을 더해 y값을 계산한다. 여기서 주의할 것은 모델 학습 과정에서 데이터는 이미 결정된 값으로 미지수나 변수가 아니다. 학습 과정에서 결정되어야 하는 변수는 모델의 파라미터인 weight이다.
이번 예시에서는 전체 학습 과정을 이해하기 쉽게 선형 관계를 갖는 1차원의 feature와 1차원의 label을 갖는 dummy data를 사용한다. 이 예시를 통해 모델이 parameter에 의해 결정된다는 것을 이해하고, 학습 과정에서 데이터의 역할과 parameter의 변화에 대해 알아보자.
데이터 준비

예시에 사용할 데이터는
이제 이 데이터를 가장 잘 설명하는 1차원 선형 모델을 찾아보자.
1차원 선형 모델
feature와 output 모두 1차원이기 때문에 이를 모사할 선형 모델은
이 예시에서 파라미터는

학습 과정에서 모델은 데이터가 존재하는 x-y의 공간이 아니라 model의 parameter의 공간에서 분석한다. 그 이유는 모델의 학습 과정에서 데이터는 이미 결정된 ‘상수’이고 최적화 과정에 개입하는 ‘변수’는 모델의 parameter이기 때문이다. 이 내용은 다음 최적화 과정을 보면 이해할 수 있다.
모델 학습, 최적화
- 모델이 학습한다는 것은 데이터에 기반한 최적화를 수행한다는 것이다.
- 최적화의 기본적인 세팅은 현재 상태를 정량화 할 수 있는 함수인 목적 함수
( ) ( ) (ˆy) (y)
목적 함수
회귀 모델에서 흔히 사용하는 loss function은 MSE
이 식은 음수가 될 수 없고, 오차가 최소일 때 0 값을 가지며 모델의 예측
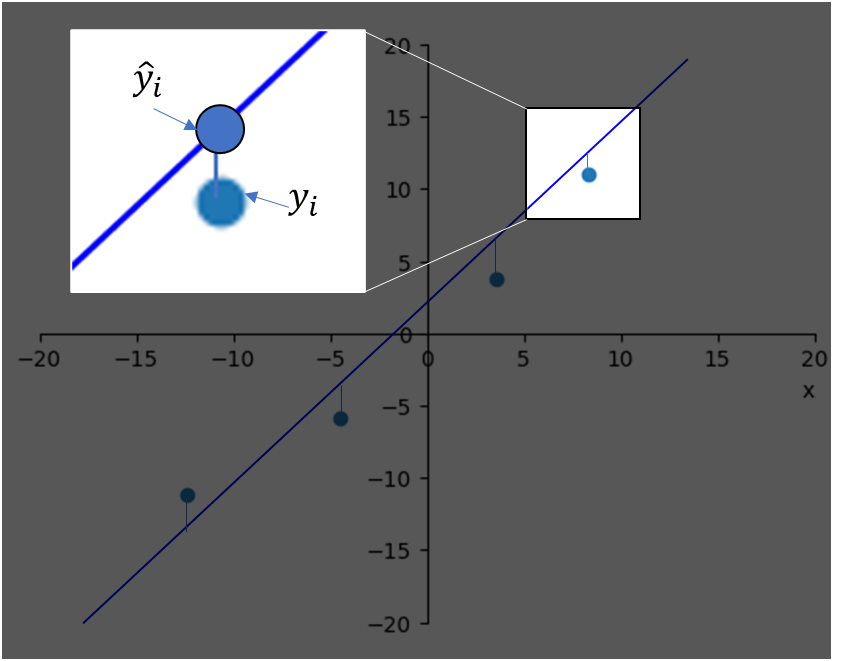
위의 식에서
최적화 알고리즘
목적 함수의 최대 혹은 최소 값을 구하기 위해 최적화 알고리즘을 적용해야 한다. 간단한 미분 가능한 함수의 경우 미분을 계산하고 그 값을 0으로 만드는 극값 중에서 최대/최소 값을 계산할 수 있지만 차원이 증가함에 따라 이런 방식으로 최적화를 수행하는 것은 불가능에 가깝기 때문에 반복적인 계산을 전제로 한다.
많은 최적화 알고리즘이 있지만 이번엔 단순히 최적 값이 있을 것으로 기대되는 구역 내에서 랜덤하게 선택된 수 많은 포인트를 계산해 비교하는 Monte carlo 방식으로 최적화를 진행해보겠다.
- 최적의
w1 w2 w1 w2 np.random.uniform(0,5, number_of_simulation)로 0과 5사이의 n개의 랜덤한 값을 샘플링 할 수 있다.
- 샘플링 된 모든 w1, w2에 대해 model을 생성하고 입력 데이터
(x) (ˆy) ( ) - 계산된 loss 값 중 가장 작은 값을 갖는 모델
( )
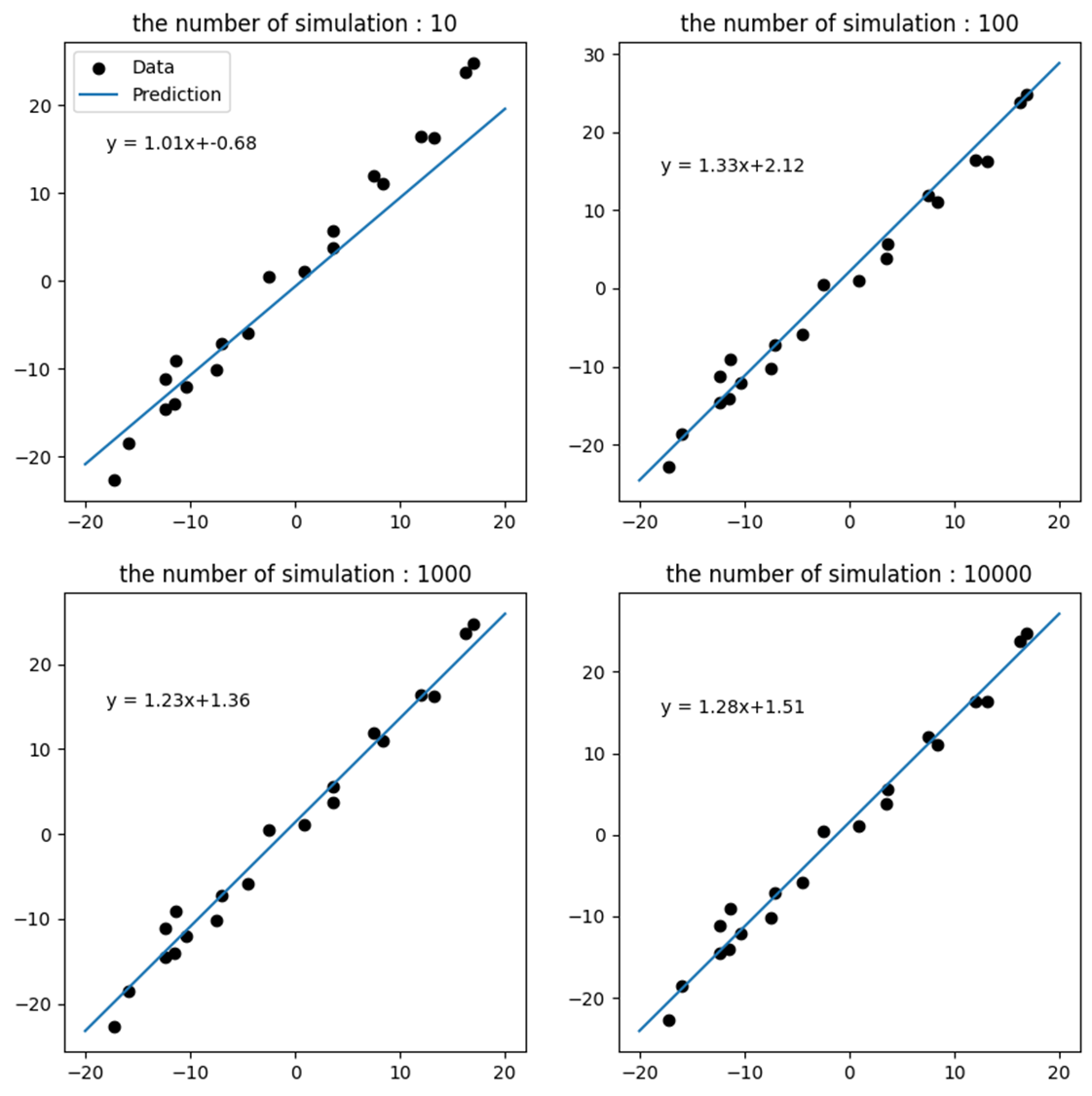
위의 그림은 monte carlo method로 찾은 최적의 모델을 실제 데이터와 함께 그린 그래프다. 좌측 상단에 위치한 100회의 simulation의 결과부터 실제 데이터를 생성한 직선과 거의 유사한 모델을 찾아내는 것을 볼 수 있다.
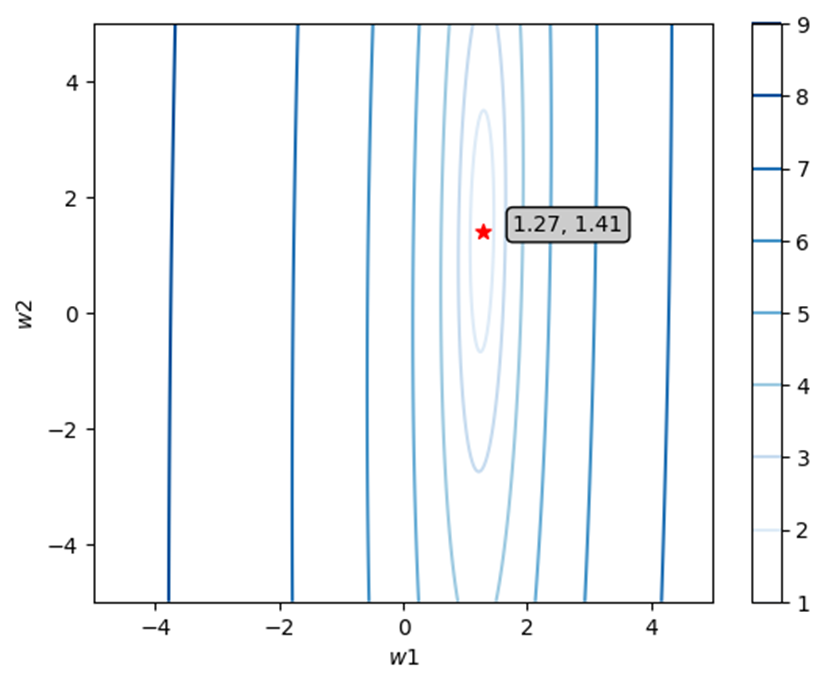
5~5 사이의 모든 w1, w2의 조합에 대한 loss 함수를 계산해 등고선 형태로 그려보면 아래와 같다. 이 예시에서 사용된 데이터에 의해 결정될 최적의 모델 파라미터는
그 이유는 우리가 데이터를 사용했기 때문에다. 우리가 모델 학습 과정에서 사용한 것은 오직 실제 함수에 대한 정보와 노이즈가 함께 포함된 데이터다. 노이즈가 없는 완벽한 데이터를 얻는 것은 불가능하기 때문에 데이터가 생성된 실제 함수를 완벽하게 찾을 수 있는 loss function을 얻을 수 없다.
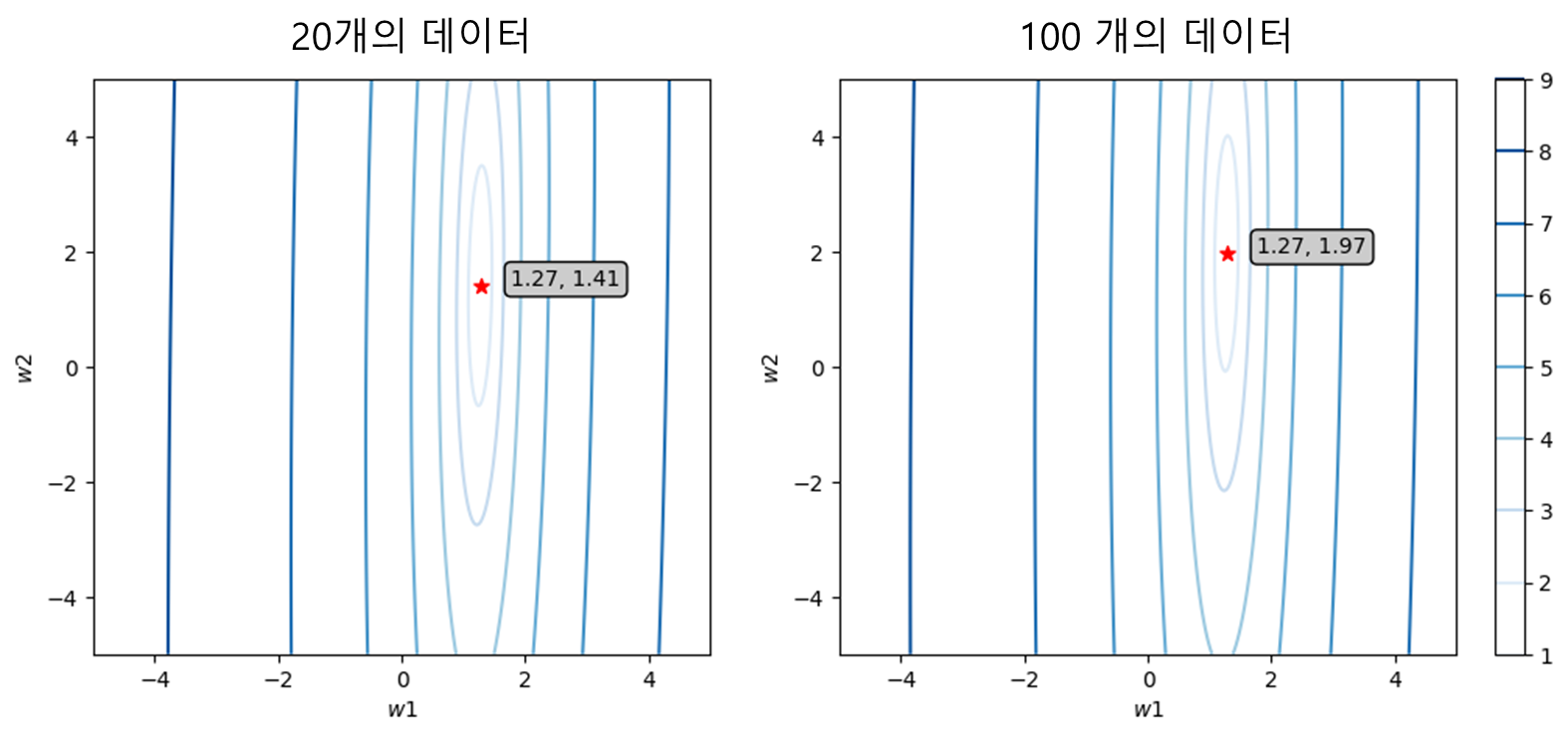
이런 노이즈의 영향을 줄일 수 있는 방법은 데이터를 추가적으로 얻는 것이다. 통계학에서 어떤 값의 평균을 추정 할 때 데이터의 수가 많을 수록 정확한 것과 같은 원리에 의해 많은 데이터는 노이즈의 영향을 줄일 수 있다. 그러나 단순히 데이터의 수가 많다고 좋다고 볼 수 없다. 데이터의 양만큼 질도 중요하다. garbage-in, garbage-out이라는 말이 있을 정도로 모델 학습의 결과는 데이터의 질에도 크게 영향을 받는다.
예제 마무리
사실 linear regression 문제는 최소 자승법
머신러닝과 python, Scikit-learn

SVM과 같이 수학적으로 이해하기도 어려운 머신 러닝 알고리즘을 학습할 때, 어떻게 구현해야할 지 막막할 수 있다. 그러나 구현 걱정은 하지 않아도 된다. python으로 구현된 scikit-learn이라는 패키지는 머신러닝 모델을 개발하는데 필요한 거의 모든 기능들이 구현되어 있다. 기본적인 개념을 익혔다면 당장 youtube나 블로그의 tutorial만 학습해 단 몇 줄의 코드로 머신러닝 모델을 구현할 수 있다.
'Data science' 카테고리의 다른 글
| Physics-based modeling과 Data-driven modeling 32 | 2024.03.01 |
|---|---|
| 신뢰성 공학 기초 0 | 2023.10.04 |
| 인공지능과 수학 4 | 2023.08.06 |
| Affine 변환 0 | 2022.07.24 |
| 최적화와 머신러닝 0 | 2022.07.24 |