신뢰성$($Reliability$)$의 공학적 정의
신뢰성$($Reliability$)$는 주어진 기간 동안 주어진 조건에서 요구 기능을 수행할 수 있는 제품$($부품/시스템)의 능력으로 운영 중에 성능에 관련된 지표다. 유사한 개념으로는 품질$($Quality$)$가 있는데, 품질은 생산 직후 제품의 성능에 관련된 지표를 나타내는 개념이다.
쉽게 말해 품질은 제품의 양품/불량품에 관한, 신뢰성은 운영 중 제품의 수명, 고장에 대한 개념으로 볼 수 있다. 제품의 성능, 사용 환경 그리고 시간에 대한 불확실한 관계를 확률적으로 정의해 Risk와 고장률 등을 분석한다. 여러 갈래로 고도화 되어 제품의 설계, 생산, 유지보수, 고장 분석 등 제품의 life cycle 전반에 활용된다.
일반적으로 신뢰성 공학의 궁극적인 목표는 부품의 고장률을 낮추고 시스템의 무중단 가동 시간을 최대화 하는 것이다.
고장$($failure$)$의 정의
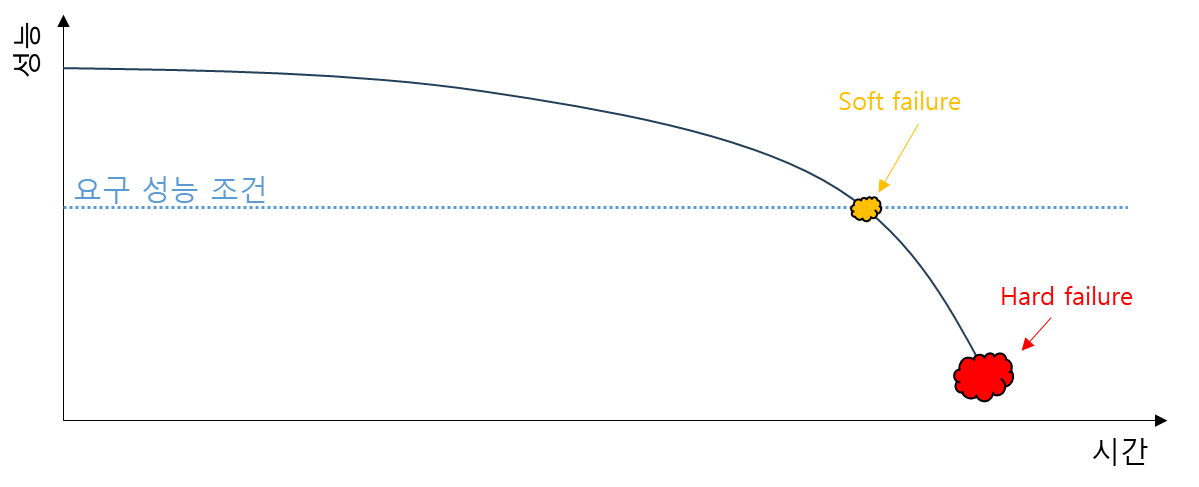
일상 생활에서 고장이라는 단어를 생각했을 때, 완전히 작동할 수 없는 상태를 생각 할 수 있다. 하지만 공학적인 정의는 ‘요구 수준’에 미치지 못하는 상태를 고장으로 정의한다. 예를 들어 타이어에 펑크가 났을 때는 당연히 고장으로 생각하지만, 교체가 필요한 시점이 도래했을 때를 고장이라고 생각하지 않는다. 그러나 공학적 정의에 따르면 해당 타이어는 요구되는 수준의 성능을 보이지 못하기 때문에 고장으로 본다.
고장을 조금 더 세분화 해 구분한다면 완전히 기능을 하지 못하는 수준의 고장은 hard failure, 요구 수준 이하로 성능이 저하된 상태의 고장은 soft failure라고 한다.
신뢰성 분석의 필요성
신뢰성 분석을 통해 제조사는 제품 보증 기간 결정, 설계 수정을 통한 신뢰성 향상 등을 짧은 개발 기간 내에 수행하고, 사용자는 TBM$($Time-based Maintenance$)$, CM$($Corrective Maintenance$)$ 등 제품의 유지 보수 방법 결정이나 경제적인 대안 제품 발굴, spare 수량 결정 등에 활용할 수 있다. 더 나아가 유지 보수 비용에 대한 수치적으로 정량화 할 수 있는 방법을 제공해 유지보수 과정에서 비용 최적화를 수행할 수 있다.
신뢰성의 측도, 신뢰성과 고장률의 확률적 정의
신뢰성의 주요 측도로 신뢰도와 고장률이 있다. 신뢰도$($reliability function$)$ $R(t)$는 앞서 언급한 신뢰성의 정의 그대로 특정 시점 t까지 고장나지 않고 요구 성능을 유지할 확률이고, 고장률$($failure rate, hazard rate$)$ $h(t)$는 멀쩡하게 기능하던 제품이 특정 시점 t에 고장이 발생할 가능성이다.
신뢰도와 고장률의 변수인 시간은 제품이 사용되는 시간으로 수명과 깊은 연관이 있다. 그런데 제품의 수명은 여러 가지 이유로 인해 불확실한 특성을 가지고 있다.

제조업 현장에서 사용되는 회전 설비에 필수적으로 사용되는 베어링을 예로 들어보자. 정밀하게 금속을 가공할 수 있는 방법과 장비로 100개의 양품 베어링을 제작한다 해도 제작 과정에서 공차$($tolerance, 허용 오차$)$ 이내로 차이가 발생한다. 뿐만 아니라 베어링을 냉동기, 압축기 등 회전 설비에 조립 과정에서, 운영 중 불확실한 조건의 부하 등의 원인으로 모든 베어링은 다른 수명을 갖는다.
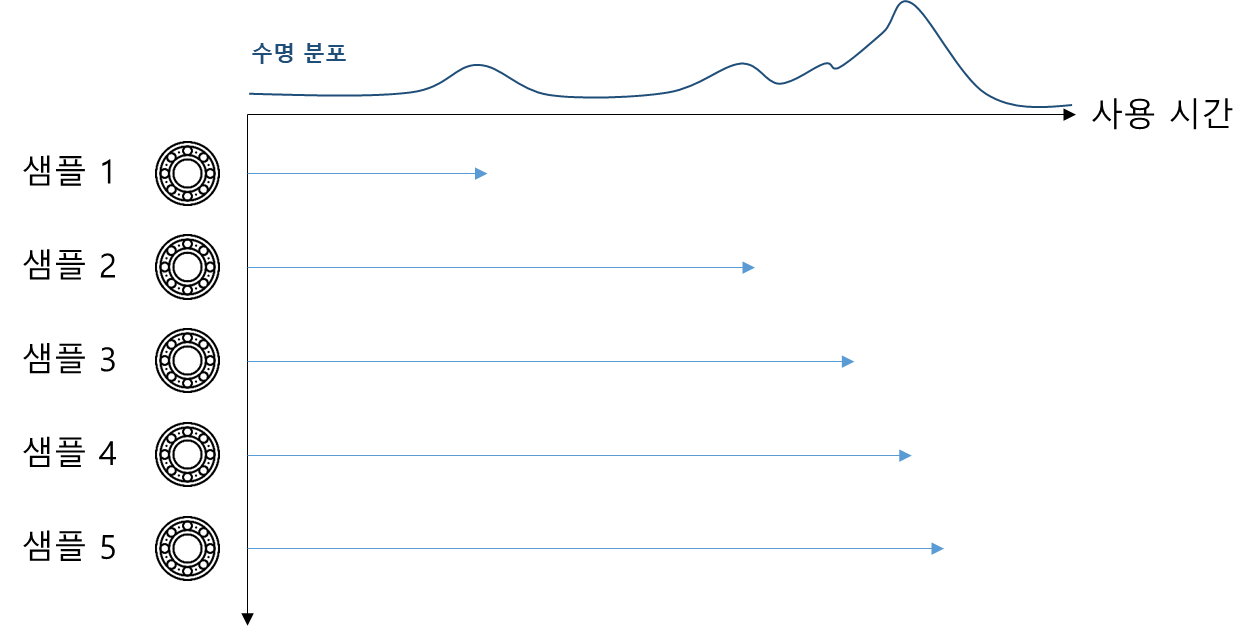
확률의 개념으로 이러한 불확실성을 정량화하고 통계적인 방법으로 제품의 신뢰성과 고장률을 모델링한다. 수명을 연속 확률 변수 $T$로 정의하고, 이의 CDF$($Cumulative distribution function$)$을 $F(t) = Pr[T \leq t]$, PDF$($Probability density function$)$를 $f(t) = \frac{d}{dt}F(t)$이라고 하자. $F(t)$는 운전 시작 후 t시점 내$($0 ~ t까지$)$에 고장이 발생할 확률, $f(t)$는 t 시점에 고장이 발생 할 가능성이라고 이해하면 된다. 수명의 PDF와 CDF를 이를 활용해 신뢰도와 고장률의 확률적인 표현을 도출해보자.
신뢰도는 특정 시점 t까지 제품이 정상 기능 수행할 확률이다. 이 말은 제품의 수명이 t보다 클 확률이므로
$$ R(t) = Pr[T>t] = 1- Pr[T\leq t]= 1-F(t) $$
고장률은 특정 시점 t까지 정상 기능을 했던 제품이, t 시점에 고장이 날 가능성이다. 조건부 확률로 정의하고 극한을 활용해 고장률 함수를 유도할 수 있다.
$$\lambda{(t)} = \lim_{\Delta t \rightarrow 0} \frac{{Pr[t< T\leq t+\Delta{t}|T>t]}}{\Delta{t}}\\
=\lim_{\Delta{t} \rightarrow 0} \frac{F(t+\Delta{t}) - F(t)}{(1-F(t))\Delta{t}}\\
= \frac{f(t)}{R(t)}
$$
위에 정의된 수식은 주저리 주저리 글로 설명한 정의에 비해 군더더기 없이 깔끔하지만 직관적으로 이해하기 어렵다. 아래 예시로 신뢰도와 고장률의 의미를 이해해보자. 아래는 최초 100개의 제품을 설치해 매년 고장이 발생한 수량을 기록한 결과와 이로부터 수명 분포$(f(t))$, 신뢰도$(R(t))$, 고장률$\lambda$을 계산 한 결과다.
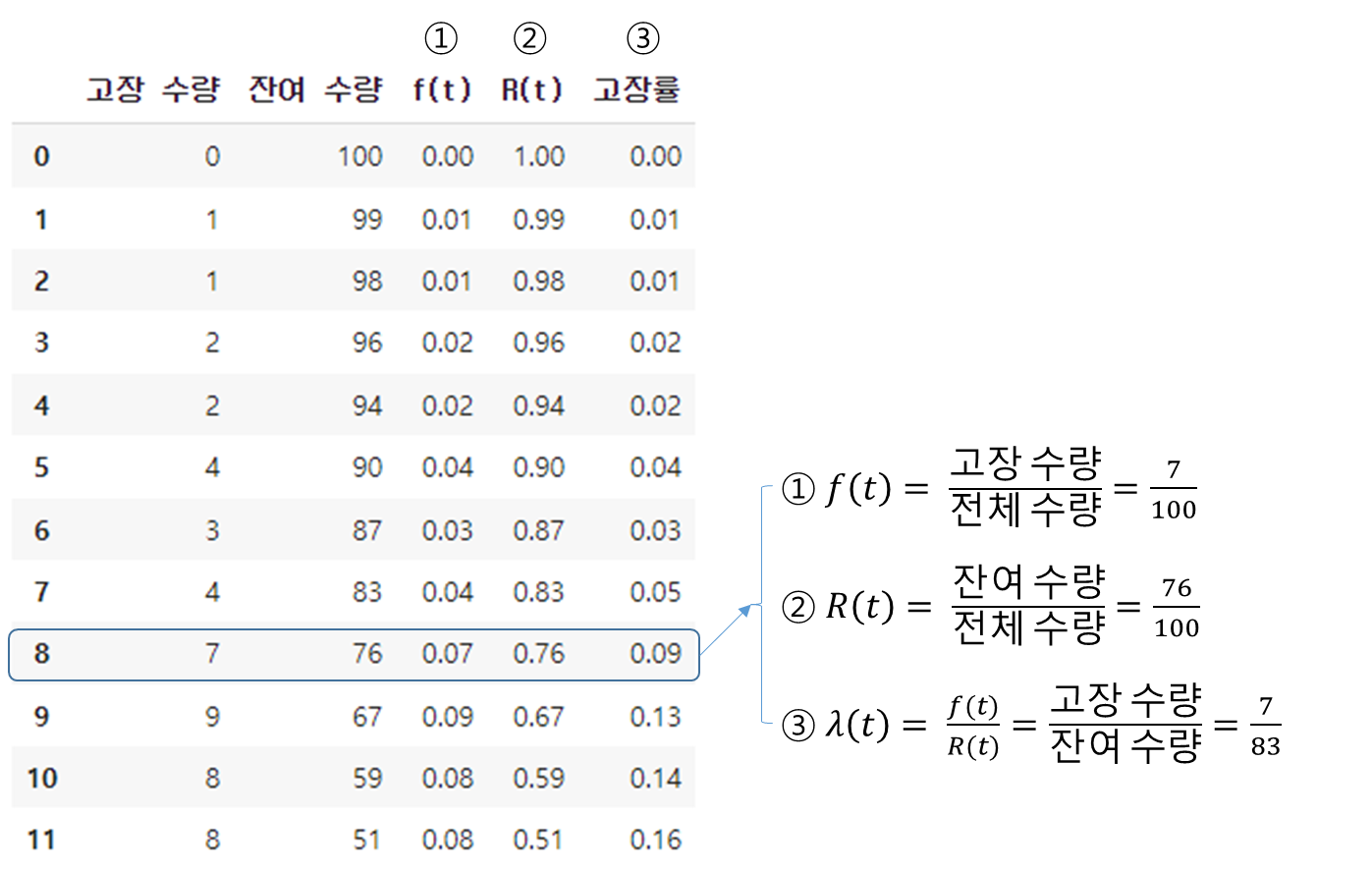
사용 8년 후에 전체 100개 중 7개의 고장이 발생해 수명 분포의 값은 0.07로 계산된다. 고장이 발생하고 남은 운영 중인 제품 수량은 76개로 신뢰도는 0.76이다. 마지막으로 고장률은 7년까지의 잔여 수량 중 고장이 발생한 제품의 수량으로 계산해 약 0.09의 값을 얻을 수 있다.
이렇게 구한 신뢰도와 고장률로 동일한 시점에 함께 제조된 제품의 신뢰성을 평가할 수 있다. 제조사에서는 이 데이터에 기반해 보증 기간이나 설계 개선 등에 활용할 수 있고, 운영사에서는 수치화 된 신뢰성 측도로 안정성과 비용 등을 함께 고려한 운영 최적화에 활용할 수 있다.
고장의 패턴, 욕조 곡선 $($bathtub curve$)$
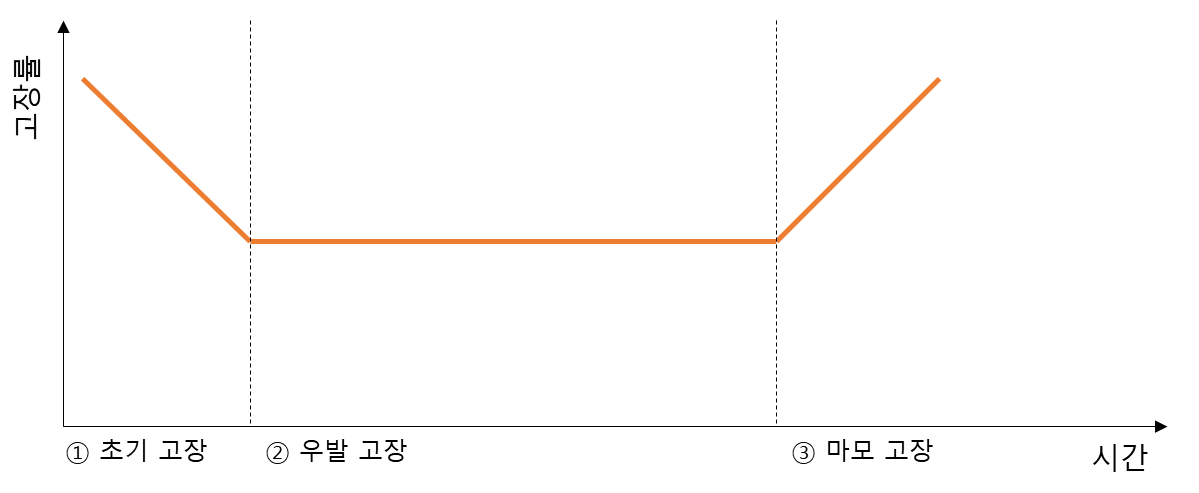
고장률의 증감 추세에 따라 고장의 패턴을 분류할 수 있다. 위 그림에서 고장률이 감소하는 구간을 ① 초기 고장$($infant failure$)$라고 한다. 이와 같은 추세는 생산 불량 등 품질에 문제가 있는 제품이 운영 초기에 고장이 발생하는 것으로 이해 할 수 있다. 제품 출고 전 burn-in test를 진행해 불량품이 출고되는 것을 막는 등의 노력으로 초기 고장률을 낮춘다.
그 이후 비교적 낮은 고장률이 유지되는 구간은 ② 우발 고장$($random failure$)$ 기간으로 유효한 사용 기간이다. 우발 고장 기간이라는 말에서 알 수 있듯 제품의 수명 도래에 의한 고장이 아니라 운영 부하의 불확실성, 사용 환경의 변화 등 외적 요인에 의한 고장이 주로 발생하는 구간이다.
마지막으로 우발 고장과 구분될 수 있는 수준으로 고장률이 증가하는 시점부터 ③ 마모 고장 $($Wear-out failure$)$이라고 한다. 마모 고장 시기에 발생하는 고장의 원인은 제품의 노후와 열화에 의한 고장이 주로 발생하기 때문에 이 시점을 제품의 수명으로 본다.
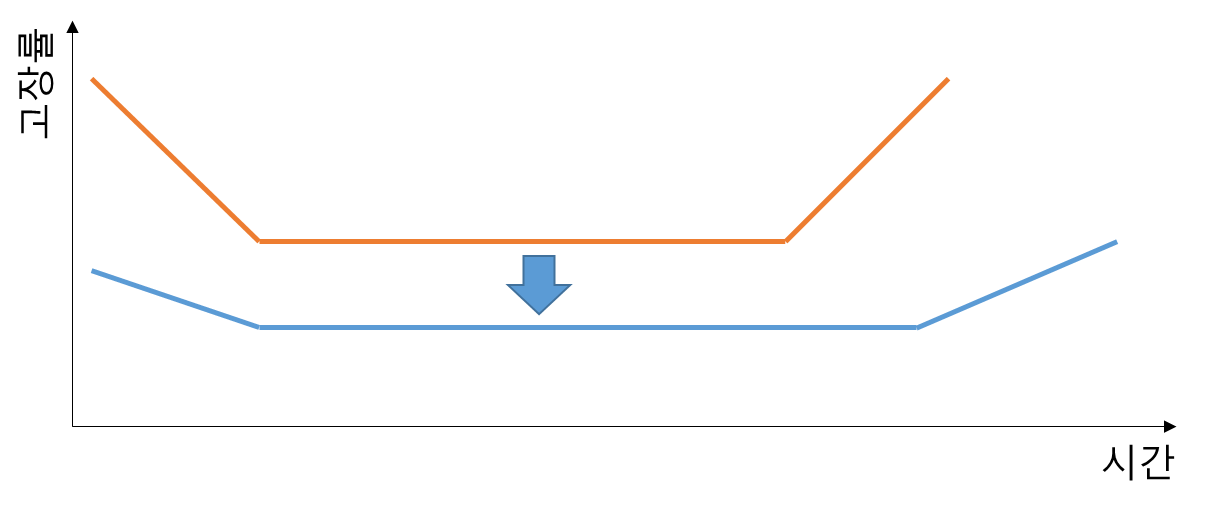
제품의 생산과 운영 과정에서 신뢰성 분석의 목표는 전체적인 고장률을 낮추고, 마모 고장 시기의 도래를 늦추는 것이다. 위의 그림에서 주황색 곡선에 비해 파란색 곡선이 더 높은 신뢰성을 갖는 형태다. 초기 고장률을 포함해 전체적인 고장률이 낮아지고, 수명의 도래로 여겨지는 마모 고장 시작 시점이 더 늦춰진 것을 볼 수 있다.
가속 수명 시험$($Accelerated Life Test, ALT$)$
제품의 신뢰성을 평가하기 위해 수명 데이터가 필요하지만, 고장이 발생할 때 까지 시험 지속이 필요하기 때문에 개발 단계에서 수행하는 것이 거의 불가능하다. 가속 수명 시험은 제품의 고장에 대한 분석을 통해 고장을 유발하는 부하와 환경 인자(온습도, 진동 등)을 도출하고, 실제 운영 조건보다 가혹한 환경에서 수명 시험을 진행한다. 이렇게 얻은 짧은 주기의 수명을 토대로 정상 운전 조건에서 수명을 추정한다.
대표적으로 온도는 많은 기계.전자 제품의 여러 고장 모드에 영향을 주는 인자로 가속 수명 시험에서 고온으로 가혹한 환경을 만드는데 많이 사용되는 방법이다.
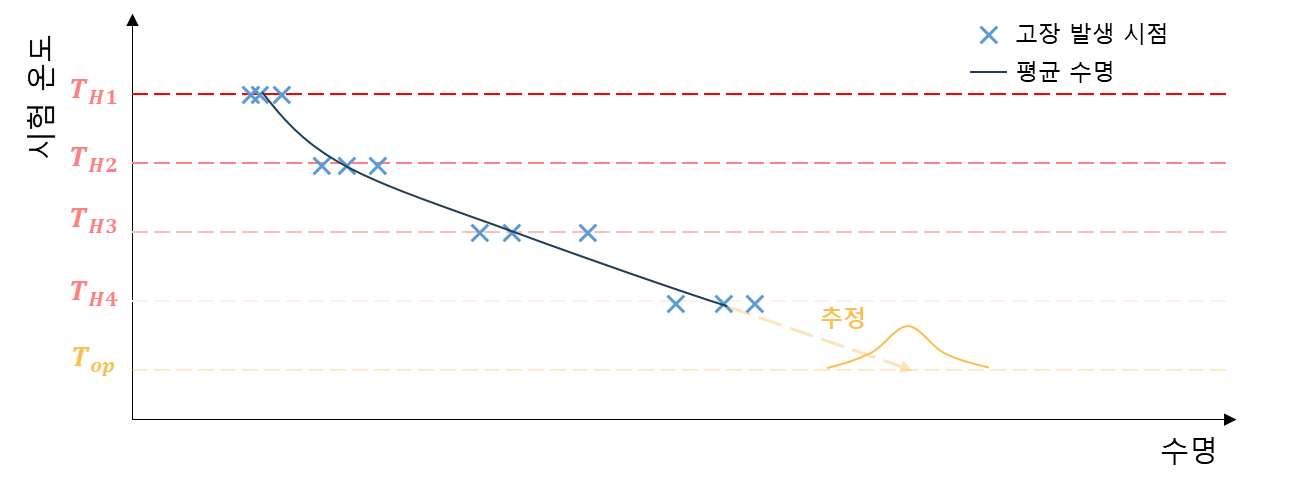
수명이 온도에 영향을 받는 경우 아레니우스 모형으로 높은 온도에서 비교적 짧은 시간 동안 수행된 수명 시험 데이터를 활용해 운영 조건에서 수명을 추정 할 수 있다. 아레니우스 모형은 온도와 수명의 관계를 두 개의 파라미터로 정의한 모델이다. 아래 관계식에서 a와 b가 추정해야하는 모델의 파라미터다.
$$\ln{t} = a + \frac{b}{T}$$
$t : Life time, T : Temperature $
운영 조건에서 수명의 추정은 아레니우스 모형의 두 개의 모수를 추정하는 회귀를 진행하는 것을 의미한다.
'Data science' 카테고리의 다른 글
| Physics-based modeling과 Data-driven modeling (32) | 2024.03.01 |
|---|---|
| 모델과 지도학습 (0) | 2023.08.30 |
| 인공지능과 수학 (4) | 2023.08.06 |
| Affine 변환 (0) | 2022.07.24 |
| 최적화와 머신러닝 (0) | 2022.07.24 |