본 포스팅은 Data-Driven Modeling: Concept, Techniques, Challenges and a Case Study$($Maki K. Habib, 2021$)$에 정리된 내용에 부연 설명을 더해 작성했습니다. 별도 출처 표기가 없는 이미지는 wikipedia의 이미지를 활용했습니다.
현실 세계의 복잡한 시스템의 행동이나 특성을 예측하기 위해 모델링을 한다. 어떤 자극이나 입력$($$x$$)$에 대해 응답 혹은 출력$($$y$$)$을 예측할 수 있는 수학적인 모델을 만들어 활용한다. 모델을 활용해 시뮬레이션, 최적화, 예측, 제어, 고장 진단 등 많은 분야에 활용할 수 있다.
이번 포스팅에서는 데이터 기반 모델링에 대한 이해를 높히는 것을 목표로 한다. 이후 모델링 접근법 분류, 모수적 데이터 기반 모델링에 대한 설명을 하고 motor modeling case study를 통해 물리 기반 모델링 방법과 데이터 기반 모델링 방법에 대한 이해를 할 수 있도록 작성했다.
Modeling Approaches

모델링 방법은 크게 물리 기반 모델링과 데이터 기반 모델링으로 나눌 수 있다.
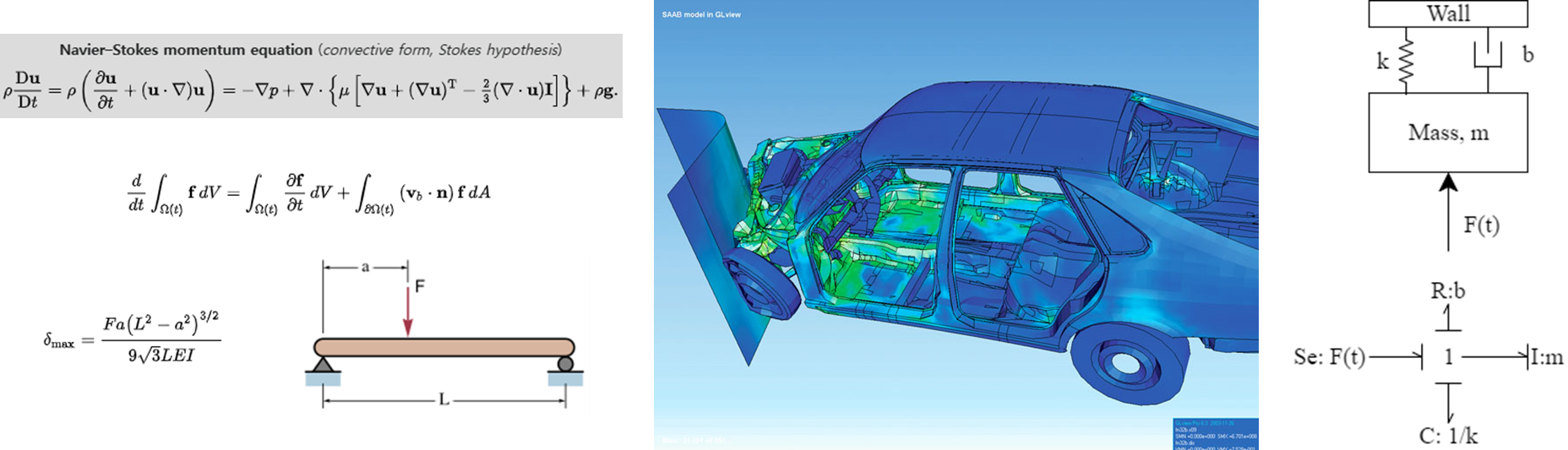
물리 기반 모델링 기법을 좀 더 세분화하면 분석적 접근$($Analytical approach$)$과 수치적 접근$($Numerical approach$)$로 구분할 수 있는데, 이는 물리의 이론적인 지식의 활용 정도로 구분된다. 분석적 접근은 질량 보존 법칙, 에너지 보존 법칙과 같이 일반적인 물리 법칙으로부터 유도한 closed-form 형태의 모델을 도출하는 방식이다. 수치적 접근은 분석적 방법으로 풀 수 없는 형태의 복잡한 문제를 모델링하는 방법이다. 대부분 물리 현상을 수학적으로 표현하는 과정에서 복잡한 미분 방정식 형태로 표현되고 Finite Element Method$($FEM$)$이나 Finite Difference Method$($FDM$)$ 등 컴퓨터를 활용해 반복 계산하는 방식으로 얻을 수 있는 모델을 도출한다. 분석적 접근과 수치적 접근 모두에서 시스템의 거동을 분석할 수 있는 물리적 지식이 필요하다는 점에서 공통점이 있다.

데이터 기반 모델링은 물리적 지식을 활용하기 보다 실험 데이터를 활용해 입력 변수와 출력 변수 사이의 관계를 직접 정의한다. 데이터 기반 모델링은 모수적 방법$($Parametric$)$과 비모수적 방법$($Non-parametric$)$으로 구분된다. 모수적 방법은 모델 종류 별로 특정한 모델 구조를 가지고 있고, 입력을 처리하는 과정에 개입하는, 조정 가능한 parameter를 갖는다. 모수적 방법은 유한한 수의 parameter를 가지고 있고, 입력과 출력 사이의 관계를 가장 잘 나타내는 parameter를 찾는 과정을 거쳐 모델이 도출된다. 비모수적 방법은 parameter가 없거나 무한한 수의 parameter를 갖는 모델의 형태다. 대표적인 모수적 방법은 통계에서 모수를 갖는 확률 분포 모델이나 선형 회귀 등이 있고, 비모수적 방법은 파라미터 수가 매우 많은 딥러닝 모델이 대표적인 예시다.
Parametric Data-Driven Modeling

모수적 데이터 기반 모델링은 위 그림과 같이 1) 실험/운영을 통한 데이터 취득, 2) 모델 선택, 3) 데이터에 가장 적합한 모델 파라미터 추정, 4) 모델 테스트와 검증 순서로 진행된다. 그리고 모델링의 성능이 원하는 수준에 도달할 때 까지 이 과정을 반복한다.
데이터 기반 모델링 방법의 성능은 데이터의 질에 매우 크게 영향을 받는다. 실험을 통해 데이터를 취득하는 경우 실험 설계 단계에서 실제로 발생할 수 있는 운영 조건을 고려해야 한다. 그리고 취득한 데이터를 분석해 이상치나 노이즈를 처리할 수 있는 전처리 과정을 거치는 것도 필요할 수 있다.
모델 선택 과정에서는 모델링을 하고자 하는 시스템의 특성에 따라 적합한 모델을 선택할 필요가 있다. 모델의 특성에 따라 크게 선형 모델과 비선형 모델로 구분 지을 수 있고, 비선형 모델이 더 복잡한 현상을 모사할 수 있다. 작은 단위의 시스템을 모델링 하는 경우 선형 모델로 충분히 모사 할 수 있기 때문에 선형 모델을 먼저 선택하고 결과를 확인해 결과가 좋지 않은 경우 비선형 모델링을 시도한다. 모델의 종류에 따라 추정이 필요한 parameter가 결정되기 때문에 이후 과정에서 선택한 모델의 종류에 따라 추정 방식이 달라진다.
모델의 파라미터 추정은 앞 단계에서 선택한 모델의 parameter를 데이터에 가장 적합하게 맞추는 과정이다. 대부분 알고리즘에서 입력 값에 해당하는 모델의 예측과 실제 데이터의 차이를 줄이는 것을 목표로 최적화를 통해 파라미터를 추정한다. 머신러닝 알고리즘에 대해서 이 과정을 **학습$($training$)$**이라고 한다.
마지막으로 개발된 모델을 다시 데이터를 활용해 평가하고 요구 수준에 맞는 모델을 얻을 때 까지 새로운 아이디어와 데이터를 추가하며 위 과정을 반복해 데이터 기반 모델링을 수행한다.
최근에는 matlab이나 python에 다양한 machine learning 모델을 활용 할 수 있는 toolbox와 library를 제공하기 때문에 데이터 취득 이후 과정은 어렵지 않게 시도 할 수 있다.
Case study : Simple DC Motor Modeling
DC motor는 간단한 dynamic system으로 아래 그림과 같이 간단한 bond graph로 모델링 할 수 있다. 공급 전력에 따라 DC motor의 회전 속도나 출력 토크를 분석할 수 있다. 이와 같은 방식은 DC motor의 동작에 대한 이해에 기반해 전류와 DC motor의 회전 속도, 토크의 관계를 정의한 물리 기반 모델이다.

여기에선 아래와 같이 DC motor의 제어 입력 신호와 출력 신호 사이 관계를 데이터 기반 기법으로 모델링하는 예시를 소개한다. motor는 pulse width modulation $($PWM$)$ 방법으로 제어되었다. PWM 제어는 일정한 전압 공급 상황에서 digital 제어$($ON과 OFF$)$만 가능 한 DC motor를 analog 제어$($출력 제어 가능$)$ 하는 방식이다. PWM은 특정 시간 주기 동안 ON 출력을 유지하는 시간의 비율$($duty cycle$)$을 조절해 출력을 제어한다. PWM의 duty cycle이 클 수록 DC motor의 출력은 커진다.
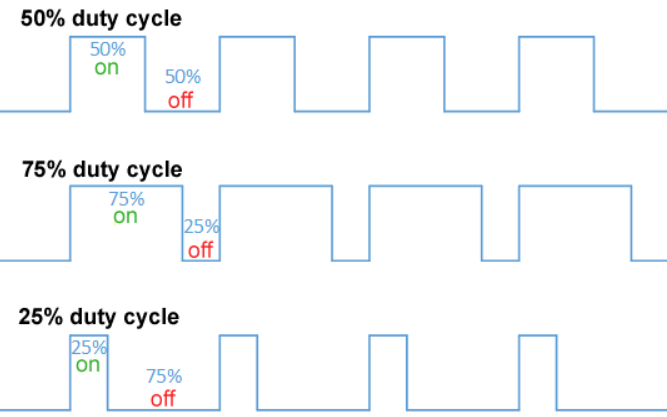
이 예시에서는 PWM duty cycle의 값으로 motor의 회전 속도를 예측할 수 있는 데이터 기반 모델을 학습시킨다.
Step1. Data aquisition
모델링에 필요한 데이터를 취득하기 위해 아래 이미지와 같이 실험 준비를 한다. 이 실험 세팅에서 데이터 기반 모델링을 활용해 모사하고자 하는 변수인 PWM duty cycle과 motor 회전 속도 데이터를 취득한다.

Duty cycle을 0에서 100%까지 변화 시키며 motor 회전 속도를 RPM 단위로 취득 했다. 0.02초의 데이터 취득 주기로 500초 동안 실험을 진행해 총 25000개의 데이터 값을 취득했다. 그 결과는 아래 그림에서 볼 수 있다.
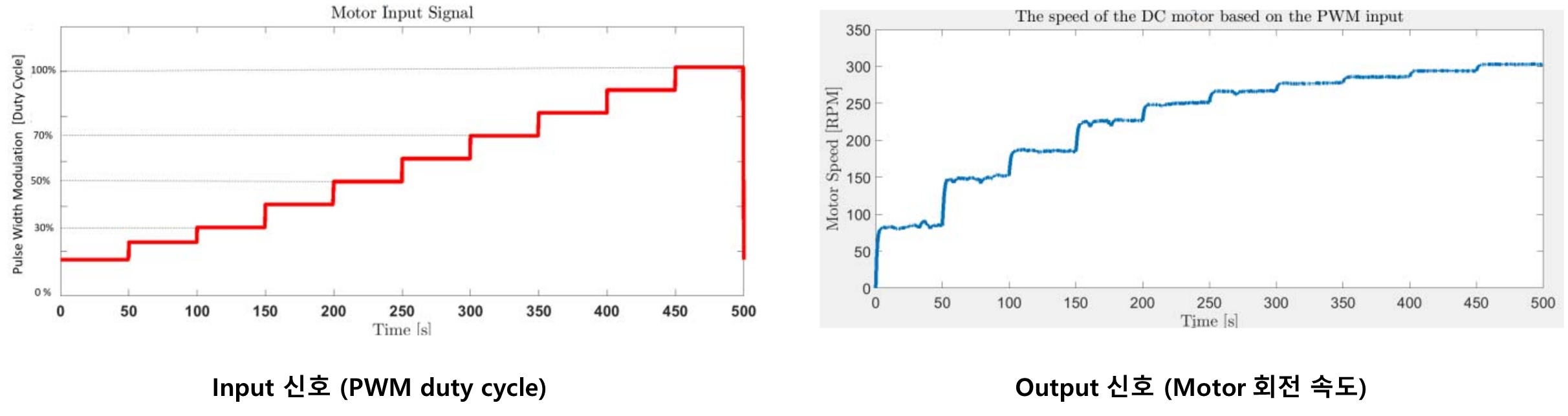
Step2. Model selection
이 사례에서 모델링을 하고자 하는 input과 output signal의 비선형성을 고려해 NARX$($Nonlinear AutoRegressive with exogenous inputs$)$를 채택했다. 아래 식은 일반적인 NARX 모델을 나타낸다.
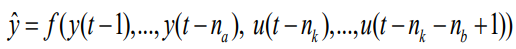
예측 변수$($$\hat{y}$$)$는 그 이전 출력 신호$($$y$$)$들과 입력 신호$($$u$$)$들의 비선형적인 함수로 예측할 수 있다는 아이디어다. 위 식에서 예측 시점을 $t$라고 했을 때 $t-1$은 예측 시점보다 하나 앞선 데이터, $t-2$는 두개 앞선 데이터를 의미한다. 따라서 $y(t-1)$은 예측 시점 직전에 취득된 출력 신호를 의미한다.
시간에 따라 변화하는 데이터 특성 상 현재 시점에서 과거 시점으로 갈 수록 예측 변수와 상관 관계는 줄어들기 때문에 적절한 길이의 데이터를 활용해야 한다. $n_a,n_b,n_k$를 조정함으로써 모델의 입력이 될 데이터의 형태를 정의할 수 있다.
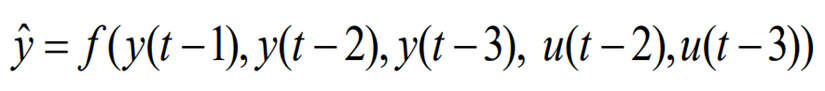
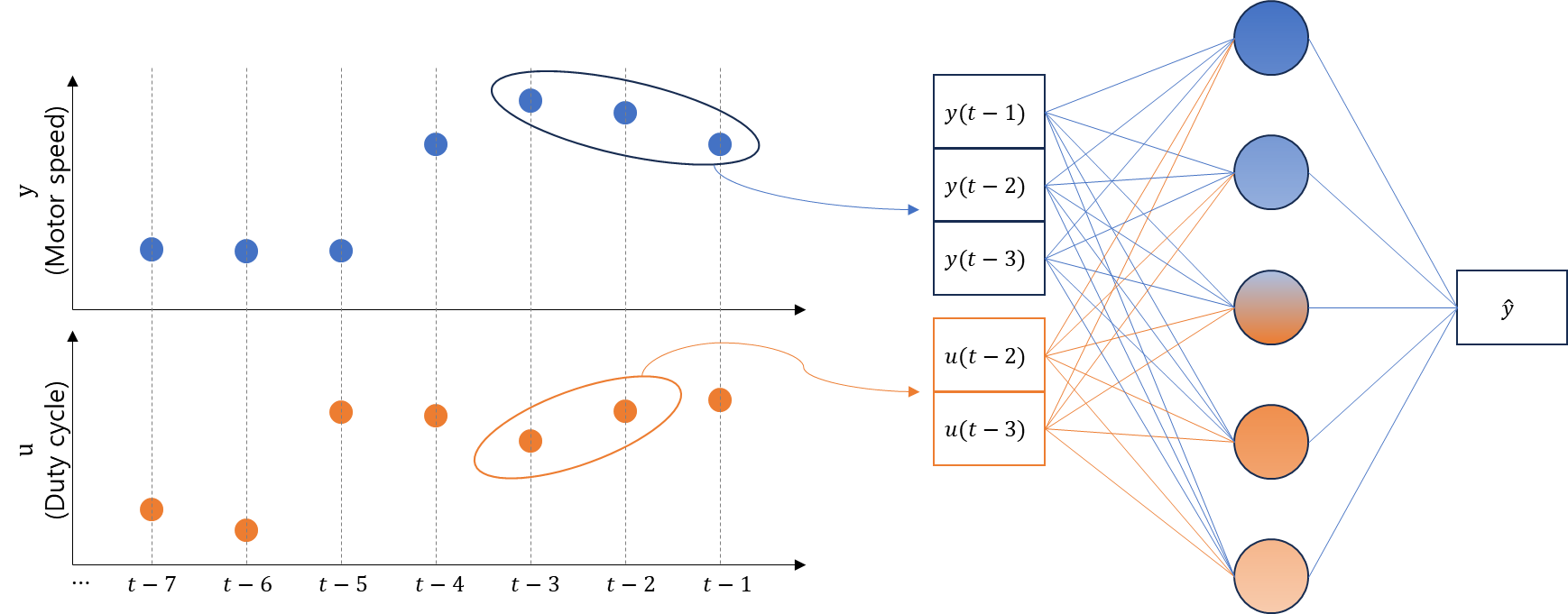
여기에선 $n_a,n_b,n_k$를 각각 3, 2, 2로 설정해 3개의 y값과 2개의 u값을 입력으로 받는 것으로 정의했다. $f$는 1개의 layer에 5개 node를 갖는 MLP$($Multi-Layer Perceptron$)$ 모델을 사용해 구현했다. 이를 그림으로 정리하면 아래 그림과 같다.
Step3. Model Training and Validation
모델 학습은 모델 파라미터를 조정해 모델의 예측과 실제 데이터의 오차를 최소화하는 최적화 과정이다. 여기에서 cost function은 회귀 문제에 널리 사용되는 MSE(Mean Squared Error)를 사용했다. 학습 과정에서는 전체 실험 데이터의 80%만을 사용했고 나머지 20%는 모델의 성능 검증하는데 사용했다.
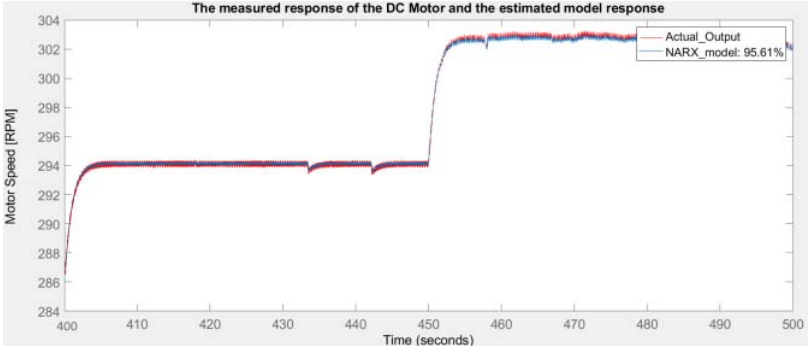
위 그림은 학습에 사용되지 않은 20%의 데이터에 대해 실제 측정 값과 모델 예측 값을 함께 도시한 결과다. 이로부터 학습된 모델이 꽤 정확하게 motor speed를 예측하고 있는 것을 확인할 수 있다.
Conclusion
본 포스팅을 통해 physics-based modeling과 data-driven modeling의 개념을 이해하고 data-driven modeling의 과정을 구체적으로 설명했다.